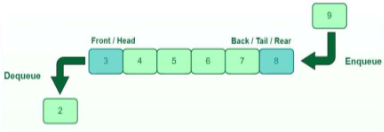
Queue - CSE205: Data Structures and Algorithms | B.Tech CSE Notes PDF | FineNotes4U

byOne -

Queue


A queue is a linear data structure that follows the First-In-First-Out (FIFO) principle. 
It operates like a line where elements are added at one end (rear) and removed from the other end (front).

⭐Queue - Array Implementation:


CODE:

#include <iostream>
using namespace std;

class Queue {
    int front, rear, size;
    int *arr;

public:
    Queue(int s) {
        front = rear = -1;
        size = s;
        arr = new int[s];
    }

    // Enqueue operation
    void enqueue(int value) {
        if (rear == size - 1) {
            cout << "Queue is full" << endl;
            return;
        }
        else{
            if(front == -1){
                front = 0;
            }
            rear++;
            arr[rear] = value;
        }
    }

    // Dequeue operation
    void dequeue() {
        if (front == -1 || front > rear) {
            cout << "Queue is empty\n";
            return;
        }
        else{
            cout << "Dequeued: " << arr[front] << endl;
            front = front + 1;
        }
    }
    
    // Peek operation
    void peek() {
        if (front == -1 || front > rear) {
            cout << "Queue is empty\n";
            return;
        } 
        else {
            cout << "Front element is: " << arr[front];
        }
    }

    // Display operation
    void display() {
        if (front == -1 || front > rear) {
            cout << "Queue is empty\n";
            return;
        }
        else{
            cout << "Queue Elements are: ";
            for (int i = front; i <= rear; i++)
                cout << arr[i] << " ";
        }
        cout << endl;
    }
};

int main() {
    Queue q(5);
    
    q.enqueue(10);
    q.enqueue(20);
    q.enqueue(30);
    q.display();
    
    q.dequeue();
    q.display();
    
    q.peek();

    return 0;
}

OUTPUT:

Queue Elements are: 10 20 30 
Dequeued: 10
Queue Elements are: 20 30 
Front element is: 20

⭐Queue - Linked List Implementation:


CODE:

#include <iostream>
using namespace std;

struct Node {
    int data;
    Node* next;
};

class Queue {
    Node *front, *rear;

public:
    Queue() {
        front = rear = nullptr;
    }

    // Enqueue operation
    void enqueue(int value) {
        Node* temp = new Node();
        temp->data = value;
        temp->next = nullptr;
        if (rear == nullptr) {
            front = rear = temp;
        } 
        else {
            rear->next = temp;
            rear = temp;
        }
    }

    // Dequeue operation
    void dequeue() {
        if (front == nullptr) {
            cout << "Queue is empty\n";
            return;
        }
        Node* temp = front;
        front = front->next;
        if (front == nullptr){
            rear = nullptr;
        }
        int removed = temp->data;
        delete temp;
        cout << "Dequeued: " << removed << endl;
    }

    // Peek operation
    void peek() {
        if (front == nullptr) {
            cout << "Queue is empty\n";
            return;
        }
        cout << "Front element: " << front->data << endl;
    }

    // Print operation
    void print() {
        if (front == nullptr) {
            cout << "Queue is empty\n";
            return;
        }
        cout << "Queue elements are: ";
        Node* temp = front;
        while (temp != nullptr) {
            cout << temp->data << " ";
            temp = temp->next;
        }
        cout << "\n";
    }
};

int main() {
    Queue q;
    
    q.enqueue(10);
    q.enqueue(20);
    q.enqueue(30);
    q.print();
    
    q.dequeue();
    q.print();
    
    q.peek();

    return 0;
}

OUTPUT:

Queue elements are: 10 20 30 
Dequeued: 10
Queue elements are: 20 30 
Front element: 20

⭐Queue – Operations:

  • Enqueue() - Insertion of elements to the queue.
  • Dequeue() - Removal of elements from the queue.
  • Peek() - Acquires the data element available at the front node of the queue without deleting it.
  • isFull() - Validates if the queue is full.
  • isNull() - Checks if the queue is empty.

⭐Priority Queue:

  • A priority queue is a type of queue that arranges elements based on their  priority values
  • Elements with higher priority values are typically retrieved before elements with lower priority values.
  • Priority queue can be implemented using the following data structures:
    • Arrays
    • Linked list

CODE:

#include <iostream>
using namespace std;

struct Node {
    int value;
    int priority;
    Node* next;
};
Node* head = nullptr;

// Insertion
void insert(int value, int priority) {
    Node* newNode = new Node();
    newNode->value = value;
    newNode->priority = priority;
    newNode->next = nullptr;

    if (head == nullptr || head->priority < priority) {
        newNode->next = head;
        head = newNode;
    } 
    else {
        Node* current = head;
        while (current->next != nullptr && current->next->priority >= priority) {
            current = current->next;
        }
        
        newNode->next = current->next;
        current->next = newNode;
    }
}

// Deletion (removes the highest priority element)
Node deleteMax() {
    if (head == nullptr) {
        cout << "Queue is empty!" << endl;
        return {-1, -1, nullptr};
    }
    Node* temp = head;
    Node deleted = {head->value, head->priority, nullptr};
    head = head->next;
    delete temp;
    return deleted;
}

// Traversal
void traverse() {
    if (head == nullptr) {
        cout << "Queue is empty!" << endl;
        return;
    }
    Node* current = head;
    while (current != nullptr) {
        cout << "(" << current->value << ", " << current->priority << ") ";
        current = current->next;
    }
    cout << endl;
}

int main() {
    insert(10, 2);
    insert(30, 3);
    insert(20, 1);
    insert(40, 5);

    cout << "Priority Queue after insertions: ";
    traverse();

    Node deleted = deleteMax();
    cout << "Deleted max: (" << deleted.value << ", " << deleted.priority << ")" << endl;

    cout << "Priority Queue after deletion: ";
    traverse();

    return 0;
}

OUTPUT:

Priority Queue after insertions: (40, 5) (30, 3) (10, 2) (20, 1) 
Deleted max: (40, 5)
Priority Queue after deletion: (30, 3) (10, 2) (20, 1) 

⭐Difference between Priority Queue and Normal Queue:

  • There is no priority attached to elements in a queue, the rule of first-in-first-out(FIFO) is implemented whereas, in a priority queue, the elements have a priority.
  • The elements with higher priority are served first.

⭐Deque (Double-ended Queue):

  • A double-ended queue (deque) is an abstract data type that generalizes a queue, for which elements can be added to or removed from either the front or rear.

  • An input-restricted deque:
    • It is one where deletion can be made from both ends, but insertion can be made at one end only

  • Output-Restricted Deque: 
    • It is a deque with some limitations while performing deletion operations
  • Four basic operations are performed on deque, they are as follows:
    • Insertion at Rear
    • Insertion at Front
    • Deletion at Front
    • Deletion at Rear

CODE:

#include <iostream>
using namespace std;

// Global variables for deque
int* arr;
int front = -1;
int rear = 0;
int currentSize = 0;
int capacity;

// Function to insert an element at the front
void insertFront(int value) {
    if (currentSize == capacity) {
        cout << "Deque is full!" << endl;
        return;
    }
    front = (front + 1) % capacity;
    arr[front] = value;
    currentSize++;
    if (rear == 0) {
        rear = front;
    }
}

// Function to insert an element at the rear
void insertRear(int value) {
    if (currentSize == capacity) {
        cout << "Deque is full!" << endl;
        return;
    }
    rear = (rear - 1 + capacity) % capacity;
    arr[rear] = value;
    currentSize++;
    if (front == -1) {
        front = rear;
    }
}

// Function to delete an element from the front
void deleteFront() {
    if (currentSize == 0) {
        cout << "Deque is empty!" << endl;
        return;
    }
    front = (front - 1 + capacity) % capacity;
    currentSize--;
    if (currentSize == 0) {
        front = -1;
        rear = 0;
    }
}

// Function to delete an element from the rear
void deleteRear() {
    if (currentSize == 0) {
        cout << "Deque is empty!" << endl;
        return;
    }
    rear = (rear + 1) % capacity;
    currentSize--;
    if (currentSize == 0) {
        front = -1;
        rear = 0;
    }
}

// Function to display the deque elements
void display() {
    if (currentSize == 0) {
        cout << "Deque is empty!" << endl;
        return;
    }
    cout << "Deque elements: ";
    for (int i = 0; i < currentSize; i++) {
        cout << arr[(front - i + capacity) % capacity] << " ";
    }
    cout << endl;
}

int main() {
    capacity=5;

    arr = new int[capacity];

    insertRear(10);
    insertRear(20);
    insertFront(30);
    display();

    deleteFront();
    display();

    insertFront(40);
    insertRear(50);
    display();

    deleteRear();
    display();

    return 0;
}

OUTPUT:

Deque elements: 30 10 20 
Deque elements: 10 20 
Deque elements: 40 10 20 50 
Deque elements: 40 10 20 

🚨Thanks for visiting finenotes4u✨

Welcome to a hub for 😇Nerds and knowledge seekers! Here, you'll find everything you need to stay updated on education, notes, books, and daily trends.

💗 Bookmark our site to stay connected and never miss an update!

💌 Have suggestions or need more content? Drop a comment below, and let us know what topics you'd like to see next! Your support means the world to us. 😍

You might like

View all
Previous Post Next Post
Share to other apps
Copy Post link