Recursion - CSE205: Data Structures and Algorithms | B.Tech CSE Notes PDF | FineNotes4U

Recursion

A function that calls itself is known as a recursive function. This technique is known as recursion.

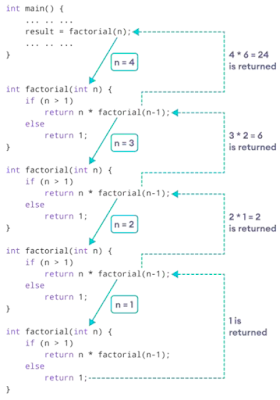
⭐Factorial of a Number:

CODE:

#include <iostream>
using namespace std;

int factorial (int n){
    if(n>1){
        return n * factorial(n - 1);
    }
    else{
        return 1;
    }
}

int main(){
    int n, result;
    n = 4;
    result = factorial(n);
    cout << result;
    return 0;
}

OUTPUT:

24

⭐Tower of Hanoi:

A few rules to be followed for Tower of Hanoi are:

• Only one disk can be moved among the towers at any given time.
• Only the 'top' disk can be removed.
• No large disk can sit over a small disk

• The minimal number of moves required to solve Tower of Hanoi puzzle of n disks would be (2^n) − 1.

CODE:

#include <iostream>
using namespace std;

void towerofHanoi(int n, char from_rod, char to_rod, char aux_rod){
    if (n==0){
        return;
    }
    towerofHanoi(n - 1, from_rod, aux_rod, to_rod);
    cout << "Move disk " << n << " from rod" << from_rod << " to rod " << to_rod << endl;
    towerofHanoi(n - 1, aux_rod, to_rod, from_rod);
}

int main(){
    int N=3;
    towerofHanoi(N, 'A', 'C', 'B');
    return 0;
}

OUTPUT:

Move disk 1 from rodA to rod C

Move disk 2 from rodA to rod B

Move disk 1 from rodC to rod B

Move disk 3 from rodA to rod C

Move disk 1 from rodB to rod A

Move disk 2 from rodB to rod C

Move disk 1 from rodA to rod C

Complexity Analysis:

Time Complexity: 

• O(2N) There are two possibilities for every disk. 
• Therefore, 2 * 2 * 2 * . . . * 2(N times) is 2N

Space Complexity: 

• O(N), Function call Stack Space

⭐Merge Sort:

CODE:

#include <iostream>
using namespace std;

// Function to merge two halves
void merge(int A[], int start, int mid, int end) {
    int n1 = mid - start + 1;
    int n2 = end - mid;

    // Create temporary arrays
    int* left = new int[n1];
    int* right = new int[n2];

    // Copy data to temporary arrays
    for (int i = 0; i < n1; i++)
        left[i] = A[start + i];
    for (int j = 0; j < n2; j++)
        right[j] = A[mid + 1 + j];

    // Merge the temporary arrays back into A[start..end]
    int i = 0;
    int j = 0;
    int k = start;

    while (i < n1 && j < n2) {
        if (left[i] <= right[j]) {
            A[k] = left[i];
            i++;
        } else {
            A[k] = right[j];
            j++;
        }
        k++;
    }

    // Copy the remaining elements of left[], if any
    while (i < n1) {
        A[k] = left[i];
        i++;
        k++;
    }

    // Copy the remaining elements of right[], if any
    while (j < n2) {
        A[k] = right[j];
        j++;
        k++;
    }

    // Free the temporary arrays
    delete[] left;
    delete[] right;
}

// Merge Sort function
void merge_sort(int A[], int start, int end) {
    if (start < end) {
        int mid = (start + end) / 2;
        merge_sort(A, start, mid);
        merge_sort(A, mid + 1, end);
        merge(A, start, mid, end);
    }
}

// Function to print the array
void printArray(int A[], int size) {
    for (int i = 0; i < size; i++)
        cout << A[i] << " ";
    cout << endl;
}

int main() {
    int A[] = {38, 27, 43, 3, 9, 82, 10};
    int size = sizeof(A) / sizeof(A[0]);

    cout << "Original array: ";
    printArray(A, size);

    merge_sort(A, 0, size - 1);

    cout << "Sorted array: ";
    printArray(A, size);

    return 0;
}

OUTPUT:

Original array: 38 27 43 3 9 82 10 

Sorted array: 3 9 10 27 38 43 82

Complexity Analysis:

Time Complexity:

• O(N log N), in all 3 cases (worst, average and best) as merge sort always divides the array into two halves and takes linear time to merge two halves.

Auxiliary Space:

• O(N), in merge sort, all elements are copied into an auxiliary array. So, N auxiliary space is required.

⭐Quick Sort:

CODE:

#include <iostream>
using namespace std;

// Function to partition the array
int partition(int arr[], int low, int high, int pivot) {
    int i = low - 1;
    for (int j = low; j < high; j++) {
        if (arr[j] <= pivot) {
            i++; 
            swap(arr[i], arr[j]);
        }
    }
    swap(arr[i + 1], arr[high]);
    return i + 1;
}

// Quick Sort function
void quickSort(int arr[], int low, int high) {
    if (low < high) {
        int pivot = arr[high];
        int pos = partition(arr, low, high, pivot);
        quickSort(arr, low, pos - 1);
        quickSort(arr, pos + 1, high);
    }
}

// Function to print the array
void printArray(int arr[], int size) {
    for (int i = 0; i < size; i++)
        cout << arr[i] << " ";
    cout << endl;
}

int main() {
    int arr[] = {10, 7, 8, 9, 1, 5};
    int size = sizeof(arr) / sizeof(arr[0]);

    cout << "Original array: ";
    printArray(arr, size);

    quickSort(arr, 0, size - 1);

    cout << "Sorted array: ";
    printArray(arr, size);

    return 0;
}

OUTPUT:

Original array: 10 7 8 9 1 5 

Sorted array: 1 5 7 8 9 10

Complexity Analysis:

Time Complexity:

• Best Case: Ω (N log N)
• Average Case: θ ( N log N)
• Worst Case: O(N^2)

Auxiliary Space:

• O(1), if we don’t consider the recursive stack space. If we consider the recursive stack space, then, in the worst-case quick sort could make O(N).

---

🚨Thanks for visiting finenotes4u✨

Welcome to a hub for 😇Nerds and knowledge seekers! Here, you'll find everything you need to stay updated on education, notes, books, and daily trends.

💗 Bookmark our site to stay connected and never miss an update!

💌 Have suggestions or need more content? Drop a comment below, and let us know what topics you'd like to see next! Your support means the world to us. 😍